작성일자 : 2023-11-19
Ver 0.1.1
0.Intro
학부생시절 통계학을 공부하면서부터 수없이도 많이 들어온 가설 검정.
헷갈릴만한 통계 용어도 꽤나 많이 등장하고, 우리 실생활에서도 리서치 등에서 사용되는 방법이므로 개념 확립을 위해 정리할 필요성이 있어 가설 검정의 과정에 대해서 정리해보고자 한다.
이번 포스팅은 유의수준 대한 내용이다.
- 귀무가설, 대립가설 수립
- 유의수준 확인
- 귀무가설 하에 검정통계량 계산
- 검정통계량으로 p-value 계산
- 귀무가설 기각 여부 결정(채택/기각)
-> 가설검정은 검정통계량을 구해 귀무가설을 채택할 것인지 기각할 것인지 판단하는 과정
1. 제 1종 오류, 제 2종 오류 그리고 검정력
유의 수준에 대해서 내용 정리를 하기 전에 먼저 정리해야할 개념 및 용어가 있다.
바로 제 1종 오류와 제 2종 오류, 그리고 검정력이다.
유의수준에 대한 설명에 앞서 지난 포스팅에서 귀무가설과 대립가설에 대해서 정리를 해보았다.
[Statistics] 귀무가설과 대립가설
작성일자 : 2023-11-18 Ver 0.1.1 0.Intro 학부생시절 통계학을 공부하면서부터 수없이도 많이 들어온 가설 검정. 헷갈릴만한 통계 용어도 꽤나 많이 등장하고, 우리 실생활에서도 리서치 등에서 사용되
junius96.com
일반적으로 주장하고자 하는 사실을 대립가설, 기각하고자 하는 사실을 귀무가설로 설정한다.
예를 들어 , A 대학교의 남학생과 여학생의 성적 평균에 차이가 있다라는 주장을 하고 싶다면 아래와 같이 가설을 설정할수 있다.
Ho : 두 집단의 성적 평균은 같다. (차이가 없다.)
H1 : 두 집단의 성적 평균은 다르다. (차이가 있다.)
대립가설이 사실이라면 귀무가설을 기각 (두 집단의 평균은 다르다.)하고, 대립가설이 거짓이면 귀무가설을 채택(두 집단의 성적 평균은 같다)한다고 결론을 내린다.
하지만 이런 결론에서도 오류의 가능성이 존재하는데,
만약 귀무가설이 참일 때, 이를 기각할 경우 제 1종 오류(Type 1 error, α)를 범했다고 하며,
귀무가설이 거짓일 때, 이를 채택할 경우 제 2종 오류(Type 2 error, β)를 범했다고 한다.
그리고 귀무가설이 거짓일 때, 귀무가설을 기각시킬 확률이 검정력(Power, 1-β)이다.
이를 도식화 하면 아래 표와 같다.
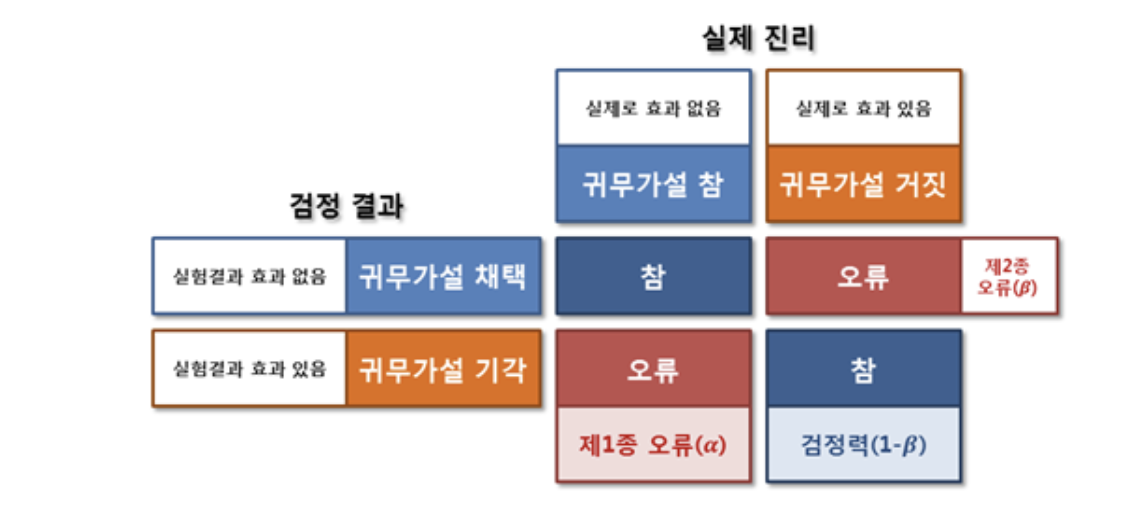
각 확률 분포표에서 위 개념들을 도식화 하면 아래와 같다.
추가로 제 1종 오류(α)와 제 2종 오류(β) 값은 반비례 or Tradeoff 관계이다.
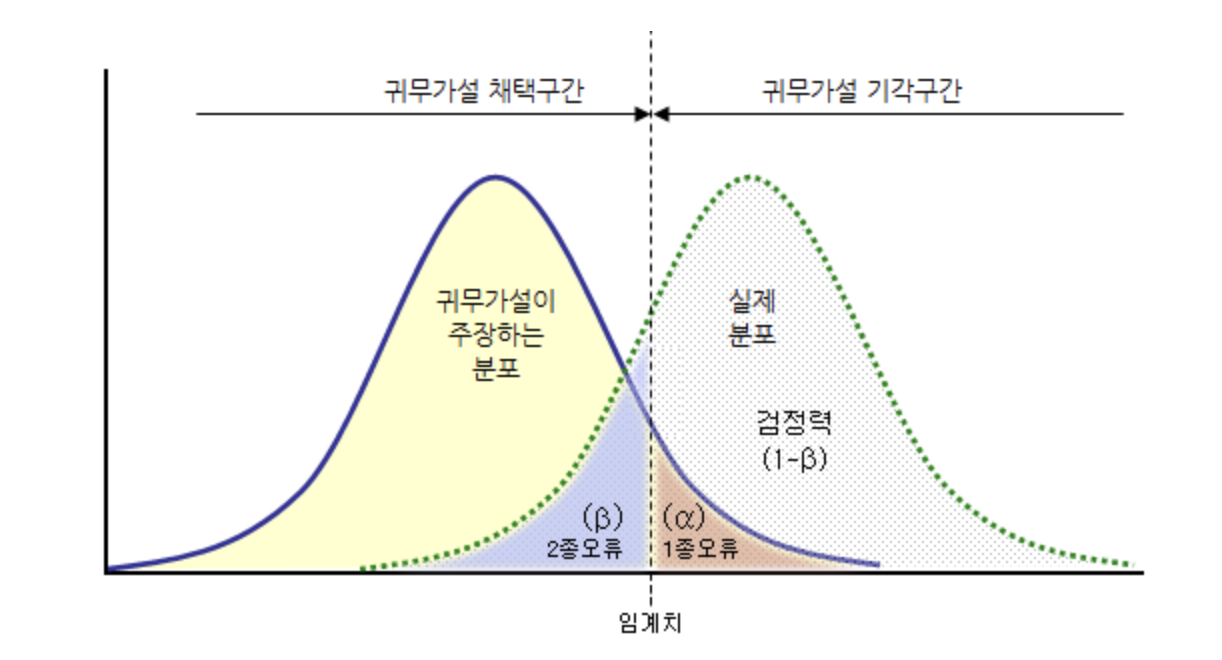
2. 유의 수준(Significance Level)이란?
앞서 제 1종 오류(α)와 제 2종 오류(β), 그리고 검정력(power)에 대해서 정리해보았다.
다시 가설 검정으로 돌아와 가설 검정에서는 제 1종 오류의 상한선을 미리 설정해두고 이를 넘지 않도록 규정하는데, 이 상한선이 바로 유의수준(Significance Level)이다.
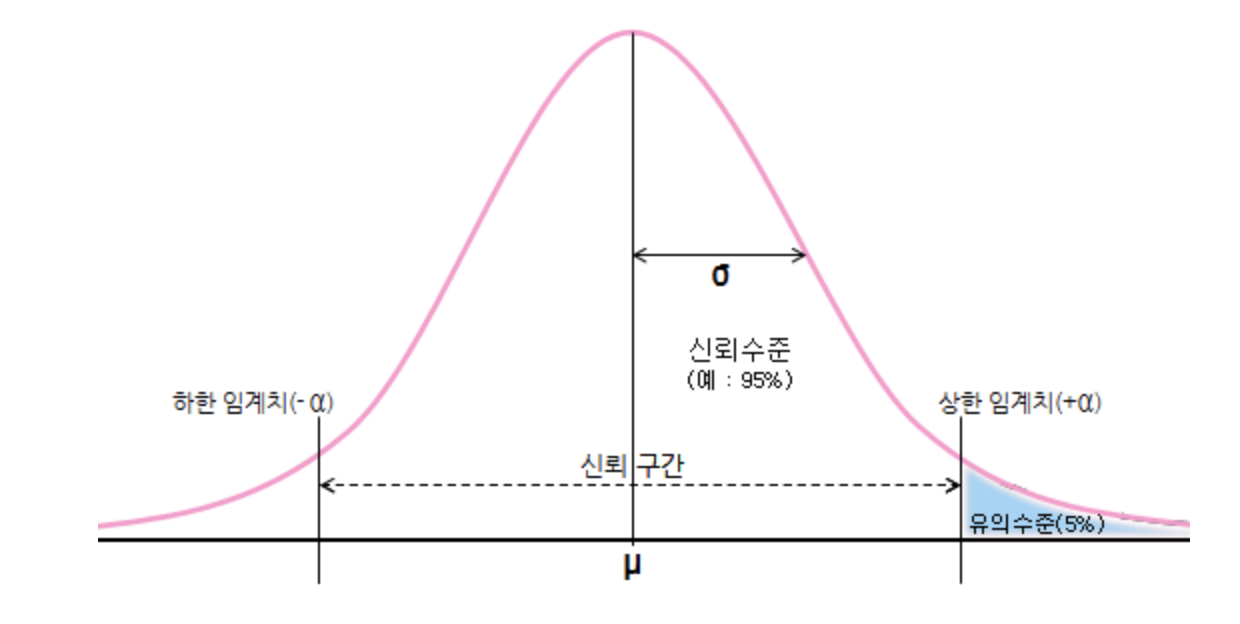
여기서 유의수준(Significance Level)은 신뢰수준(Confidence Level)의 반대말로도 해석된다.
예를들어 유의수준이 0.05이라고 한다면 신뢰수준이 0.95 즉 95%의 신뢰도라고 해석할 수 있다는 것이다.
앞서 제 1종 오류(α)와 제 2종 오류(β) 값은 반비례 or Tradeoff 관계이라고 했고, 유의수준은 신뢰수준의 반대말이라고 했다.
위 개념들간의 관계를 정리를 하면 아래와 같다
- 유의 수준 ∝ 1 / 신뢰 수준
- 유의 수준 ∝ 검정력
- 신뢰 수준 ∝ 1 / 제 1종 오류(α)
- 유의 수준 ∝ 제 1종 오류(α) (1,2의 삼단논법)
- 검정력 ∝ 1 / 제 2종 오류(β)
표본의 크기가 커질수록 검정통계량이 커지므로, 귀무가설의 기각이 쉬워지고, 이에 통상적으로 제 1종 오류, 제 2종 오류 두가지 오류를 모두 줄이려면 표본의 크기를 늘려야 한다.
